Concepto intuitivo de límite
Si los valores de f(x) pueden hacerse arbitrariamente cercanos a un número (único) L, cuando x se acerca a un número «a» por izquierda y por derecha, entonces decimos que el Límite de f(x) es L cuando x tiende a «a» y lo expresamos así:

Vamos a utilizar GeoGebra para explicar el concepto intuitivo de límite. Estudiaremos el comportamiento de la función que esta puesta en la imagen cuando «x» toma valores muy próximos a «1» por izquierda y por derecha.
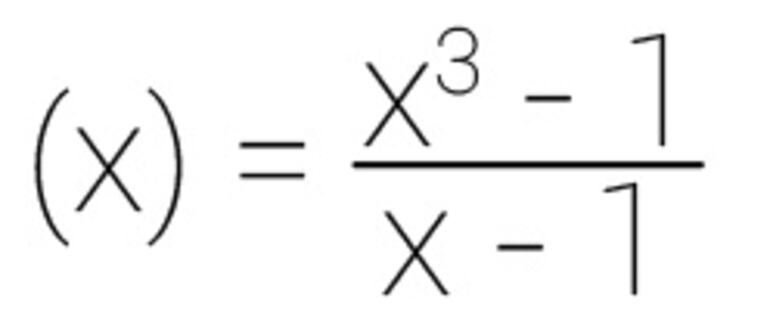
Para ello realizamos la siguiente construcción:
a) Ingresamos en la barra de entrada la siguiente función:
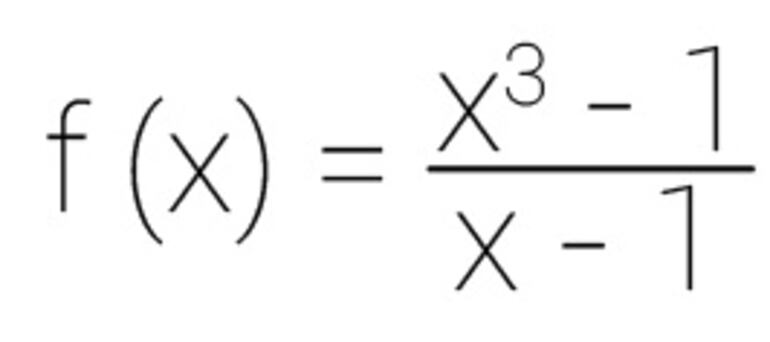
b) Creamos dos deslizadores del tipo número:
«a» que varíe de 0 a 0,99 con un incremento de 0,01, creciente y velocidad 0.5.
«b» que varíe de 1,01 a 2 con un incremento de 0,01, decreciente y velocidad 0.5.
c) Creamos los siguientes puntos:
A(a, f(a)) y B(b, f(b)) puntos sobre la función f.
C(a,0) y D(b,0) proyecciones de A y B sobre el eje x.
E(0,f(a)) y F(0,f(b)) proyecciones de A y B sobre el eje y.
d) Trazamos los segmentos AC, AE, BD y BF y modificamos el estilo (línea de puntos).
e) Ingresamos en entrada los siguientes valores:
- LI = y(E) representa el límite de la función por izquierda.
- LD = y(F) representa el límite de a función por derecha.
Luego arrastramos estos valores desde la vista algebraica hasta la vista gráfica.

f) Haciendo clic derecho sobre los deslizadores seleccionamos Activar animación.
g) Ingresamos en entrada, el punto (1,4) y cambiamos el color a blanco.
h) Por último, podemos agregar elementos de texto dinámico a la construcción y lo subimos a nuestro perfil.
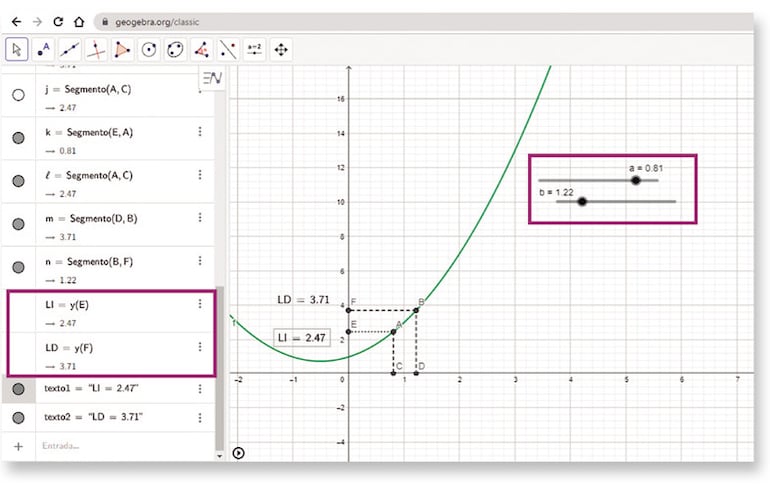
Existen tres comandos en Geogebra que se utilizan para el cálculo de límites:
Límite izquierda[ <Función>, <Valor> ] , determina el límite lateral izquierdo de la función en el punto indicado.
Límite derecha[ <Función>, <Valor> ] , determina el límite lateral derecho de la función en el punto indicado.
Límite[ <Función>, <Valor> ], determina el límite de la función en el punto indicado.
