Paolo Ruffini: Nació el 22 de septiembre de 1765 en Valentano, Estados Papales, y murió el 10 de mayo de 1822 en Módena, actual Italia. Su padre, Basilio Ruffini, era médico en Valentano. De niño parecía destinado a la carrera religiosa. Su familia se mudó a Reggio, en el ducado de Módena, al norte de la actual Italia y Paolo entró en la universidad de Módena en 1783 para estudiar matemáticas, medicina, filosofía y literatura. Paolo Ruffini es conocido como el descubridor del llamado método de Ruffini que permite hallar los coeficientes del polinomio que resulta de la división de un polinomio cualquiera por el binomio x-a. Sin embargo, no fue esta su mayor contribución al desarrollo de la matemática. Hacia 1805 elaboró una demostración de la imposibilidad de la solución general de las ecuaciones algebraicas de grados quintos y superiores, aunque cometió ciertas inexactitudes que serían corregidas por el matemático noruego Niels Henrik Abel.
Pasos a seguir para aplicar la “Regla de Ruffini”
.Tomamos de ejemplo la división:
(x4 − 3x2 + 2) : (x − 3)
Todos los beneficios, en un solo lugar Descubrí donde te conviene comprar hoy
1. Si el polinomio no es completo, lo completamos añadiendo los términos que faltan con ceros.
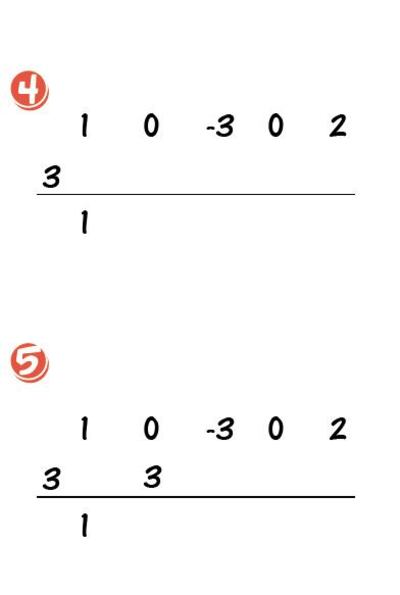
2. Colocamos los coeficientes del dividendo en una línea.
3. Abajo a la izquierda colocamos el opuesto del término independiente del divisor.
4. Trazamos una raya y bajamos el primer coeficiente.
5. Multiplicamos ese coeficiente por el divisor y lo colocamos debajo del siguiente término.
6. Sumamos los dos coeficientes.
7. Repetimos el proceso anterior.
Volvemos a repetir el proceso.
Volvemos a repetir.
8. El último número obtenido, 56, es el resto.
9. El cociente es un polinomio de grado inferior en una unidad al dividendo y cuyos coeficientes son los que hemos obtenido. x3 + 3 x2 + 6x +18
Ejemplo de una división exacta, en la forma clásica y aplicando la Regla de Ruffini.
Fuente:
Recuperado de: http://es.wikipedia.org/wiki/Paolo_Ruffini
http://www.taringa.net/posts/apuntes-y-monografias/4561381/Division-de-polinomios-Ruffini.html
Encontrarás más actividades en el Suplemento de Tareas para la Casa.